Cournot Duopoly Model | Cournot-Nash Equilibrium

Cournot Duopoly Model

The duopoly’s Cournot model is an economic model that focuses on how firms set prices and output levels when they compete with each other in the market.

The model was developed by French mathematician Antoine A. Cournot in 1838, who created this mathematical equation to predict the equilibrium point between two competing entities.

The duopoly’s Cournot model is a mathematical representation of the strategic interaction between two firms that compete for market share.

In this case, we will be looking at a duopoly that consists of two companies that supply identical products for sale or production.

Cournot-Nash Equilibrium

The Cournot-Nash equilibrium is an economic theory that states that when a market consists of several firms in a market, that the firms will be able to reach an equilibrium where they produce the same amount of goods. This theory is based on the assumption that firms do not solely focus on maximizing output but instead aim to maintain a competitive advantage.

Nash equilibrium & Cournot-Nash equilibrium

The Nash equilibrium is a situation in which no player can improve their payoff by changing strategies. In contrast, the Cournot-Nash equilibrium is when no player can improve their payoff by producing more output. In this case, the Cournot-Nash equilibrium occurs when one firm produces an arbitrarily low amount of output. If two firms produce the same output amount, there will be no change in the output level.

Cournot theorized that there is no equilibrium in pricing in a duopoly. The duopoly is the perfect example of a contested market because it is not perfect competition. The two companies in the duopoly can only set prices and quantities based on what the other firm is doing. If one company increases the price of its goods, then the other company will do the same.

The only equilibrium that exists for this situation is where both firms choose their quantity so that their marginal revenue equals their marginal costs. If one firm produces at a higher level than this, they will be punished by market forces which will cause them to lose out on profits as the competitor will take over sales and maximize profits instead.

The Nash Equilibrium is a solution to an economic game where all players act rationally and pursue their self-interests. The Cournot model of duopoly states that when firms compete on price, they produce less than the amount they would produce if there were no competition (i.e., monopolies).

A Cournot-Nash equilibrium is a type of Nash equilibrium that can be found in the competitive market when two firms are competing for customers. The model is used to predict the quantity of output and price in duopoly markets with constant marginal costs.

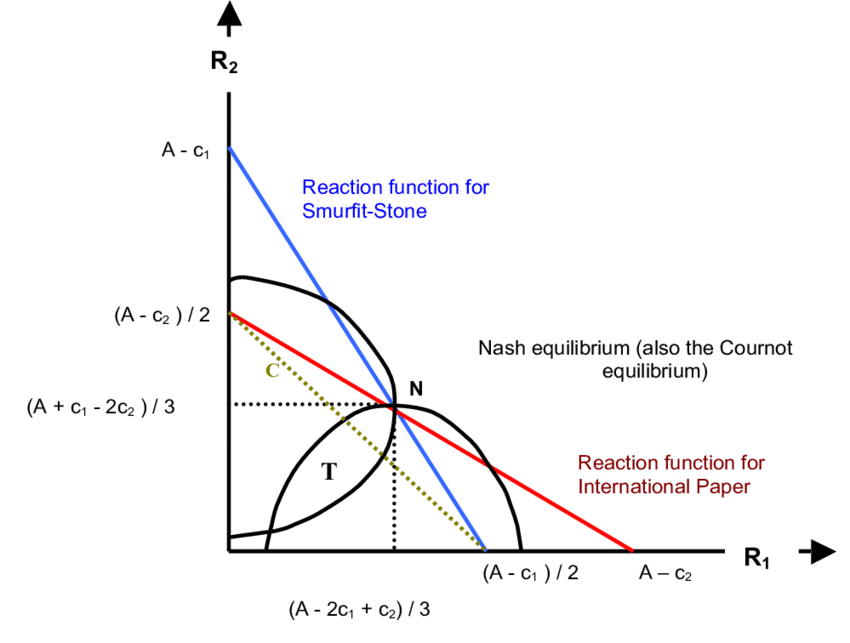
The equilibrium relies on the assumption that firms act independently and rationally, which will result in each firm producing where MR=MC.

This model’s most important assumption is that each firm has complete knowledge about what other firms are doing, but not about their own actions. Other assumptions are;

• All firms produce a homogenous product.
• The market price is therefore the result of the total supply (same price for all firms)
• Firms decide simultaneously how much to produce.
• Quantity is the strategic variable.
• The equilibrium concept used is Nash Equilibrium (Cournot-Nash)

Cournot-Nash equilibrium occurs when two sellers compete in an industry and set their prices such that the quantity supplied by each is equal to the demand by the other. This model can easily be solved mathematically from the demand and supply curves.

In the Cournot duopoly model, we assume there are two firms (firms 1 and 2). The equation gives the market demand: P1Q1 + P2Q2 = QD(qd is the total quantity demanded, and QD is the total quantity supplied).

The firms decide how much to produce based on their cost function where K1 and K2 are their costs of producing 1 unit. The firms will set their product prices such that: (1-p)K1+K2 = (q-qd)K1+K2. The equation’s market price is P = K(1 – p)K1 + K2.

 

 

Modeling anything in the real world requires us to make some assumptions, and a duopoly model is no different. One of the assumptions we made is that firms do not collude. We assume that the firms are competing with each other and aim to maximize profits.

In reality, this might not be the case for two reasons:

• Coordination failure;
• Firms might be able to reduce their costs by coordinating together (e.g., setting equal prices).

Cournot’s duopoly model is very useful in predicting the behavior of two firms under asymmetric information. It assumes that each firm may know only its own cost curves while its competitor knows all the others. This will lead to a situation where the first firm’s price and output decisions are influenced by its competitor’s price and output decisions.

On the other hand, if all firms know each other’s cost curves, the model will predict that new entrants will not enter a duopoly market because it is very costly, making competitive businesses non-profitable.

The Cournot duopoly model and its extensions are useful in explaining the growth of corporations in monopoly markets. In these markets, new firms do not have high entry costs as they cannot discriminate between market conditions and production costs. The model can also be applied in many other fields, such as the pricing of natural monopolies and common resources.